How to Write MathematicsSuppose you are deciding whether to approve or decline a visa application. You run a test to assess whether the applicant presents a risk. Let us suppose that the test is accurate 90% of the time (regardless of whether the result is positive or negative). That is, 10% of the time the test returns a false negative or a false positive. You know that visa applications are declined rarely and about 95% are approved. If your test result comes back positive (the applicant presents a risk), what are the chances that the applicant will be declined on investigation? Do you think it is approximately:
To work out the answer, we use Bayes’ theorem, which tells us how to find the probability of event A given event B, written In this case, event A is the event that you decline the application and event B is the event that the test is positive (the applicant presents a risk). In our example, 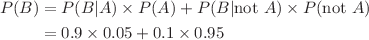 This gives We can also calculate the probability of a false negative. That is, the risk assessment test returns a negative result, indicating that applicant does not present a risk, even though the applicant actually does. Applying Bayes theorem, |
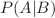 , in terms of the probability of B given A, written
, in terms of the probability of B given A, written 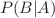 , and the probabilities of A and B:
, and the probabilities of A and B:
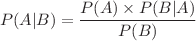
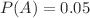 and
and 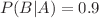 . We can derive
. We can derive 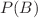 — the probability of a positive test — by adding the probabilities of a true positive test on a decline and a false positive test on an approval.
— the probability of a positive test — by adding the probabilities of a true positive test on a decline and a false positive test on an approval.
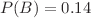 and so from equation
and so from equation 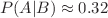 . In other words, the correct answer is (d) — you are more than twice as likely to see a false positive than a true positive.
. In other words, the correct answer is (d) — you are more than twice as likely to see a false positive than a true positive.
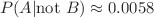 — about 0.6%.
— about 0.6%.